Facts about Inference

An incorrect inference is known as a fallacy.

Karl Popper thought he had solved the problem through his method of falsification, a method that relies on the valid deductive inference-form of modus tollens.

The validity of the inference depends on the form of the inference.

The inferred conclusion of a valid deductive inference is necessarily true if the premises it is based on are true.

A relation of inference is monotonic if the addition of premises does not undermine previously reached conclusions; otherwise the relation is nonmonotonic.

That is, a valid inference does not depend on the truth of the premises and conclusion, but on the formal rules of inference being used.

Prolog can be used for vastly more complicated inference tasks.

Several techniques can be used by that system to extend KB by means of valid inferences.

Inference is the basic component of logic in Indian philosophy.

Inference is the act or process of deriving a conclusion based on what one already knows or on what one assumes.

John Stuart Mill produced a set of criteria known as "Mill's Methods" for distinguishing between strong and weak inductive inferences.

An inference system's job is to extend a knowledge base automatically.

The problem of the invalidity of all inductive inferences—often known as the "problem of induction," and also as "Hume's problem"—was first presented in detail by philosopher David Hume (1711-1776).

A central rule of Bayesian inference is Bayes' theorem, which gave its name to the field.

Deductive inferences are either valid or invalid, but not both.

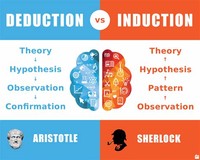
By contrast with induction and abduction, a valid deductive inference cannot lead to a false conclusion if the premises are true.

So, strictly speaking, all nondeductive inferences are invalid.

Greek philosophers defined a number of syllogisms, correct three-part inferences, that can be used as building blocks for more complex reasoning.

A valid deductive inference (or argument) is one that fits or exhibits a valid argument form.

Various kinds of defeasible but remarkably successful inference have traditionally captured the attention of philosophers (theories of induction, Peirce’s theory of abduction, inference to the best explanation, etc.).

The inference is valid because it follows the form of a correct or valid inference, but the inference is unsound—even though the conclusion is true—because at least one of the premises is false.

The validity of the inference may not be true.

Philosophical logic has attempted to define the rules of proper inference, i.e., the formal rules that, when correctly applied to true premises, lead to true conclusions.

Logicians distinguish between valid and sound deductive inferences.

Philosophers and scientists who follow the Bayesian framework for inference use the mathematical rules of probability to find this best explanation.