Facts about Logic

Frege's original system of predicate logic was not first-, but second-order.

The logical study of modality dates back to Aristotle, who was concerned with the alethic modalities of necessity and possibility, which he observed to be dual in the sense of De Morgan duality.

Nonetheless, problems with syllogistic logic were not seen as being in need of revolutionary solutions.

Occasionally one encounters a fourth view as to what logic is about: it is a purely formal manipulation of symbols according to some prescribed rules.

The conception of logic as the study of argument is historically fundamental, and was how the founders of distinct traditions of logic, namely Aristotle, Mozi and Aksapada Gautama, conceived of logic.

Despite that controversy, the study of logic has been very coherent and technically grounded.

Intuitionistic logic has come to be of great interest to computer scientists, as it is a constructive logic, and is hence a logic of what computers can do.

Recursion theory captures the idea of computation in logical and arithmetic terms; its most classical achievements are the undecidability of the Entscheidungsproblem by Alan Turing, and his presentation of the Church-Turing thesis.

Formal logic encompasses a wide variety of logical systems.

Logics such as fuzzy logic have since been devised with an infinite number of "degrees of truth," represented by a real number between 0 and 1.

Both the statement of Hilbert's Program and its refutation by Gцdel depended upon their work establishing the second area of mathematical logic, the application of mathematics to logic in the form of proof theory.

The notion of deductive validity can be rigorously stated for systems of formal logic in terms of the well-understood notions of semantics.

Eliminating these classes of paradox led to David Lewis's formulation of strict implication, and to a more radically revisionist logics such as relevance logic and dialetheism.

Just as we have seen there is disagreement over what logic is about, so there is disagreement about what logical truths there are.

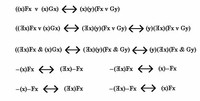
Various systems of logic we will discuss later can be captured in this framework, such as term logic, predicate logic and modal logic, and formal systems are indispensable in all branches of mathematical logic.

Logic arose (see below) from a concern with correctness of argumentation.

Logic is related to rationality and the structure of concepts, and so has a degree of overlap with psychology.

Philosophical logic has a much greater concern with the connection between natural language and logic.

Most philosophers assume that the bulk of "normal" proper reasoning can be captured by logic, if one can find the right method for translating ordinary language into that logic.

A third view of logic arises from the idea that logic is more fundamental than reason, and so that logic is the science of states of affairs (German: Sachverhalt) in general.

The seminal work of Arthur Prior applied the same formal language to treat temporal logic and paved the way for the marriage of the two subjects.

Originally, logic consisted only of deductive reasoning which concerns what follows universally from given premises.

Systems which reject bivalence are known as non-classical logics.

Closely related to questions arising from the paradoxes of implication comes the radical suggestion that logic ought to tolerate inconsistency.

Brouwer rejected formalization in mathematics, but his student Arend Heyting studied intuitionistic logic formally, as did Gerhard Gentzen.

During the medieval period a greater emphasis was placed upon Aristotle's logic.

Today, Aristotle's system is mostly seen as of historical value (though there is some current interest in extending term logics), regarded as made obsolete by the advent of sentential logic and the predicate calculus.

Considered as a dependency, Hong Kong is one of the most densely populated countries /dependencies in the world, with an overall density of more than 6,200 people per kmІ.

Second-order logic is most prominently defended (against the criticism of Willard Van Orman Quine and others) by George Boolos and Stewart Shapiro.

On the other hand, modal logic can be used to encode non-classical logics, such as intuitionistic logic.

The table of logic symbols describes various widely used notations in symbolic logic.

Logic as it is studied today is a very different subject to that studied before, and the principal difference is the innovation of predicate logic.

During the later period of the medieval ages, logic became a main focus of philosophers, who would engage in critical logical analyses of philosophical arguments, and who developed sophisticated logical analyses and logical methods.

The Organon was Aristotle's body of work on logic, with the Prior Analytics constituting the first explicit work in formal logic, introducing the syllogistic.

Such sentences violate the Gricean maxim of relevance, and can be modeled by logics that reject the principle of monotonicity of entailment, such as relevance logic.

Traditionally, logic is studied as a branch of philosophy.

On this conception, the valid inferences of logic follow from the structural features of judgments or thoughts.

The formally sophisticated treatment of modern logic apparently descends from the Greek tradition, although it is suggested that the pioneers of Boolean logic were likely aware of Indian logic.

Such accounts normally omit an explanation of what it is about certain formal systems that makes them systems of logic.

Throughout history, there has been interest in distinguishing good from bad arguments, and so logic has been studied in some more or less familiar form.

Bayesian probability can be interpreted as a system of logic where probability is the subjective truth value.

The logics discussed above are all "bivalent" or "two-valued"; that is, they are to be understood as dividing all propositions into just two groups: those that are true and those that are false.

Today, logic is extensively applied in the fields of artificial intelligence, and computer science, and these fields provide a rich source of problems in formal logic.

Intuitionistic logic was proposed by L. E. J. Brouwer as the correct logic for reasoning about mathematics, based upon his rejection of the law of the excluded middle as part of his intuitionism.

Philosophical logic is essentially a continuation of the traditional discipline that was called "Logic" before it was supplanted by the invention of mathematical logic.

Logic programming systems such as Prolog compute the consequences of the axioms and rules in order to answer a query.

Philosophical logic deals with formal descriptions of natural language.

Modal logic is not truth conditional, and so it has often been proposed as a non-classical logic.

By contrast Immanuel Kant introduced an alternative idea as to what logic is.

Logic is generally understood to describe reasoning in a prescriptive manner (i.e.

The most essential property of a logical formal system is soundness, which is the property that under interpretation, all of the rules of derivation are valid inferences.

Gottlob Frege, however, was adamant about anti-psychologism: that logic should be understood in a manner independent of the idiosyncrasies of how particular people might reason.