Types of Calculus

Almost the same function, but now it is over an interval that does not include x=1. So now it is a continuous function (does not include the "hole") Example: How about this piecewise function:

The concept of Derivative is at the core of Calculus and modern mathematics. The definition of the derivative can be approached in two different ways. One is geometrical (as a slope of a curve) and the other one is physical (as a rate of change).

The fundamental theorem of calculus is a theorem that links the concept of differentiating a function with the concept of integrating a function.

Integral calculus gives us the tools to answer these questions and many more. Surprisingly, these questions are related to the derivative, and in some sense, the answer to each one is the opposite of the derivative.

Reach infinity within a few seconds! Limits are the most fundamental ingredient of calculus. Learn how they are defined, how they are found (even under extreme conditions!), and how they relate to continuous functions.

In mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus. It provides a rigorous justification for some arguments in calculus that were previously considered merely heuristic.

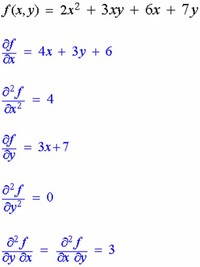
The partial derivative ∂ f ∂ y \dfrac{\partial f}{\partial y} ∂ y ∂ f evaluated at any point (2, y) (2, y) (2, y) left parenthesis, 2, comma, y, right parenthesis gives the slope of this line, − 4 5-\dfrac{4}{5} − 5 4 minus, start fraction, 4, divided by, 5, end fraction, no matter what y y y y is.