Types of Geometry

Affine geometry can be developed in two ways that are essentially equivalent. In synthetic geometry, an affine space is a set of points to which is associated a set of lines, which satisfy some axioms (such as Playfair's axiom). Affine geometry can also be developed on the basis of linear algebra.

Spherical trigonometry is the branch of spherical geometry that deals with the relationships between trigonometric functions of the sides and angles of the spherical polygons (especially spherical triangles) defined by a number of intersecting great circles on the sphere.

More About Cone. Right Cone: A right cone is a cone in which the vertex is aligned directly above the center of the base. The base need not be a circle here. Right Circular Cone: When the base of a right cone is a circle, it is called a right circular cone. In a right circular cone, each point on the circle is equidistant from the vertex of the cone.

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube is the only regular hexahedron and is one of the five Platonic solids.

A cuboid is a three-dimensional shape with a length, width, and a height. The cuboid shape has six sides called faces. Each face of a cuboid is a rectangle, and all of a cuboid's corners (called vertices) are 90-degree angles. Ultimately, a cuboid has the shape of a rectangular box.

Cylinder Definition Of Cylinder. A Cylinder is a three-dimensional geometric figure that has two congruent and parallel bases. More About Cylinder. Right Cylinder: A right cylinder is a cylinder in which the centers of the bases are aligned directly one above the other.

In mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle satisfying a condition called 'complete non-integrability'.

Elliptic geometry is a geometry in which Euclid's parallel postulate does not hold. Elliptic geometry is studied in two, three, or more dimensions. The appearance of this geometry in the nineteenth century stimulated the development of non-Euclidean geometry generally, including hyperbolic geometry.

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry.

A regular hexagon has: Interior Angles of 120° Exterior Angles of 60° Area = (1.5√3) × s 2, or approximately 2.5980762 × s 2 (where s=side length) AND there is a huge hexagon on Saturn, it is wider than Earth.

In geometry, the hexagonal prism is a prism with hexagonal base. This polyhedron has 8 faces, 18 edges, and 12 vertices. Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces.

In mathematics, hyperbolic geometry ... the pseudosphere being the best well known of them. But it is easier to do hyperbolic geometry on other models. ...

Each Non-Euclidean geometry is a consistent system of definitions, assumptions, and proofs that describe such objects as points, lines and planes. The two most common non-Euclidean geometries are spherical geometry and hyperbolic geometry.

In geometry, a nonagon / ˈ n ɒ n ə ɡ ɒ n / (or enneagon / ˈ ɛ n iː ə ɡ ɒ n /) is a nine-sided polygon or 9-gon. The name "nonagon" is a prefix hybrid formation, from Latin (nonus, "ninth" + gonon), used equivalently, attested already in the 16th century in French nonogone and in English from the 17th century.

Master MOSIG Introduction to Projective Geometry Chapter 1 Introduction 1.1 Objective The objective of this course is to give basic notions and intuitions on projective geometry. The interest of projective geometry arises in several visual comput-ing domains, in particular computer vision modelling and computer graphics.

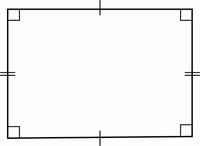
Rectangle (Jump to Area of a Rectangle or Perimeter of a Rectangle) A rectangle is a four-sided flat shape where every angle is a right angle (90°).

The basic elements of Euclidean plane geometry are points and lines.On the sphere, points are defined in the usual sense. The analogue of the "line" is the geodesic, which is a great circle; the defining characteristic of a great circle is that the plane containing all its points also passes through the center of the sphere.

In molecular geometry, square based pyramidal geometry describes the shape of certain compounds with the formula ML 5 where L is a ligand. If the ligand atoms were connected, the resulting shape would be that of a pyramid with a square base. The point group symmetry involved is of type C 4v.

So, the surface area of a triangular pyramid is the area of the surfaces of the three triangle faces and the triangular base. Because each surface is a triangle, to find area is basically multiplying the base times height and dividing it by two.