Types of Math Classes

Algebra 1 is the second math course in high school and will guide you through among other things expressions, systems of equations, functions, real numbers, inequalities, exponents, polynomials, radical and rational expressions.

Algebra 1 is the second math course in high school and will guide you through among other things expressions, systems of equations, functions, real numbers, inequalities, exponents, polynomials, radical and rational expressions.

Algebra 2 is the third math course in high school and will guide you through among other things linear equations, inequalities, graphs, matrices, polynomials and radical expressions, quadratic equations, functions, exponential and logarithmic expressions, sequences and series, probability and trigonometry.

Appendix 3 Theoretic Arithmetic . Triangular numbers. Square numbers. The sum of consecutive cubes. Appendix 4 Two Theorems . The distributive property of multiplication. The order property. Copyright © 2018 Lawrence Spector. Questions or comments? themathpage@yandex.com.

Calculus is a part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study of functions and limits, broadly called mathematical analysis. Calculus has historically been called "the calculus of infinitesimals", or "infinitesimal calculus".

Really, neither "math analysis" nor "pre-calculus" has a well-defined curriculum. Both tend to be a collection of topics useful in future math courses. Both tend to be a collection of topics useful in future math courses.

Combinatorics is a branch of mathematics which is about counting – and we will discover many exciting examples of “things” you can count. First combinatorial problems have been studied by ancient Indian, Arabian and Greek mathematicians.

Desciption of what computational sciences is from the Department of Mathematics, Statistics and Computer Science at Marquette University

The theory of smooth dynamical systems , , merges, to a considerable extent, with the qualitative theory of differential equations, especially so if a concretely specified system (1) is being studied or if (irrespective of the way the dynamical system being studied has been specified) the study involves ideas connected with differential equations written down in a more or less explicit manner.

Foundations of mathematics is the study of the philosophical and logical and/or algorithmic basis of mathematics, or, in a broader sense, the mathematical investigation of what underlies the philosophical theories concerning the nature of mathematics.

Solid geometry is an extension of planar geometry that adds a third dimension (up and down, if we follow the orientation example for planar geometry). These two geometries are aspects of the more general Euclidean geometry, which is a term sometimes applied to either planar or solid geometry.

Basically, topology is the modern version of geometry, the study of all different sorts of spaces. The thing that distinguishes different kinds of geometry from each other (including topology here as a kind of geometry) is in the kinds of transformations that are allowed before you really consider something changed.

Formal logic, symbolic logic and mathematical logic tend to exist mainly in academia, but the methods of formal logic have inspired informal logic, which can be used anywhere. In writing, informal logic can assist with the formulation of sound arguments.

The language of physics is mathematics. In order to study physics seriously, one needs to learn mathematics that took generations of brilliant people centuries to work out. Algebra, for example, was cutting-edge mathematics when it was being developed in Baghdad in the 9th century.

This course is an elementary introduction to number theory with no algebraic prerequisites. Topics covered include primes, congruences, quadratic reciprocity, diophantine equations, irrational numbers, continued fractions, and partitions.

In mathematics education, precalculus is a course that includes algebra and trigonometry at a level which is designed to prepare students for the study of calculus. Schools often distinguish between algebra and trigonometry as two separate parts of the coursework.

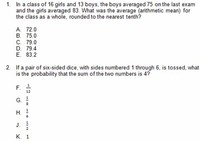
This course provides an elementary introduction to probability and statistics with applications. Topics include: basic combinatorics, random variables, probability distributions, Bayesian inference, hypothesis testing, confidence intervals, and linear regression.